Никогда не делайте гимнастику для глаз

Никогда не делайте гимнастику для глаз.

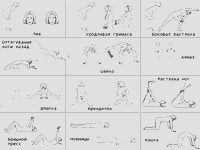
Этот комплекс незаменим для тех, кто утром с трудом открывает глаза. Хочу отметить, что если Вы постоянно будете выполнять гимнастику для глаз днем, то со временем почувствуете, что глаза утром стали открываться намного легче.

Комплекс состоит из следующих простых действий:

Этот комплекс должен занимать у Вас примерно 10 минут, из них около 5 должен занимать пальминг.

Основной комплекс гимнастики для глаз

Многие на своем опыте убедились, что если с юности выполнять такой комплекс ежедневно утром и вечером, то можно сохранить превосходное зрение на долгие годы и никогда не пользоваться очками.

Перед началом упражнений выберите удобную позу. Будет здорово, если Вы расположитесь на гимнастическом коврике, но можно сесть и на стул. Выпрямите позвоночник. Все мышцы, кроме тех, что обеспечивают сидячее положение, должны быть расслаблены. Особое внимание уделите мышцам лица. Смотрите прямо перед собой. Важно: при выполнении упражнений не допускайте перенапряжения мышц глаз. Обратите внимание на то, что движения глаз должны быть  плавными.

Упражнение 1.

Вертикальные движения глазами. Голову держите прямо, смотрите перед собой. Направьте взгляд вверх, затем – глаза вниз. Не задерживайте глаза в верхнем и нижнем положении.

Выполните упражнение 8–10 раз.

Упражнение 2.

Горизонтальные движения. Смотрите вперед. Переведите взгляд влево, потом медленно и плавно переведите его вправо.

Выполите упражнение 8–10 раз.

Упражнение 3.

Круговые движения глазами. Смотрите перед собой. Опустите глаза вниз и затем плавно поверните их по часовой стрелке до самого верхнего положения (до 12 часов). Не задерживаясь, продолжайте поворот глаз по часовой стрелке вниз (до 6 часов). Движение глаз плавное! Начинайте второй круг, не задерживая глаза в нижнем положении.

Выполните 8–10 кругов по часовой стрелке и 8–10 кругов – против. Чтобы глаза не переутомились, немного поморгаете.

Теперь закройте глаза и повторите эти же движения под закрытыми веками.

Упражнение 4.

Смотрите перед собой. При выполнении упражнения не допускайте перенапряжения глазных мышц. Движения должны быть плавными, а линия, по которой Вы ведете глаза четкой.

Перемещайте глаза в такой последовательности: верхний левый угол, нижний левый, верхний правый угол, нижний правый. Выполните упражнение 8–10 раз

Теперь проделайте то же самое в другом направлении: нижний левый угол, верхний левый, нижний правый угол, верхний правый. Выполните упражнение 8–10 раз

Поморгайте часто-часто, чтобы расслабить глаза.

Упражнение 5.

Медленно направьте свой взгляд в межбровье, на несколько секунд задержите глаза в таком положении. Также медленно переместите глаза в исходное положение и закройте их на 5-10 секунд. Со временем увеличиваете задержку глаз в верхнем положении. Но ни в коем случае не спешите, делайте это постепенно! Начинайте увеличивать задержку спустя 2-3 недели.

Упражнение 6.

Посмотрите на кончик носа. Задержите глаза в таком положении на несколько секунд затем верните их в начальное положение. Закройте глаза на небольшое время. Так же как и в упражнении 5, увеличивайте постепенно задержку.

Комплекс заканчивается выполнением пальминга (3-5 минут).

Рекомендации по выполнению гимнастики для глаз в течение дня:

1. Утром выполняйте утренний комплекс, если чувствуете, что глаза открываются с трудом. Если же глаза утром открываются легко, то делайте основной комплекс. Я делаю основной комплекс после завтрака, что бы глаза успели немного привыкнуть к свету.

2. Если Ваша работа связана с нагрузкой на глаза (например, работа за компьютером или с документами), то обязательно делайте перерывы через каждые 1-2 часа. В перерыве покиньте рабочее место: подойдите к окну, а лучше вообще выйти на улицу.

Уделите несколько минут Вашим глазам:

- сделайте одно-два упражнения для расслабления глаз

- проделайте несколько простых упражнений, вовлекающих в работу мышцы спины, шеи, плечевого пояса

3. Вечером сделайте основной комплекс гимнастики для глаз.

Важно! Если у Вас есть какие-либо нарушения зрения, то перед выполнением гимнастики обязательно проконсультируйтесь с лечащим врачом.

С уважением, Батаев Павел

Дети, конечно, звереют от окриков: "Немедленно выключи телевизор. Глаза испортишь!" Но ведь родители правы: зрение ребенка и без того перегружено. Не секрет, что 49% выпускников школ у нас страдают близорукостью. То есть, каждому второму подростку с младых ногтей уже требуются очки.

Пик ухудшения зрения приходится на старшие классы, когда ребенку надо не только усваивать новые знания, но и готовиться к школьным экзаменам, и к поступлению в институт. В этот, можно сказать, самый ответственный момент жизни глаза и дают сбой. А начинается все со зрительного утомления. Потом падает острота зрения, снижается работоспособность. Усталость глаз нередко дает о себе знать и сильными головными болями.

И что же делать родителям? А совет прост: не позволяйте детям по многу часов проводить у экранов телевизоров и компьютеров. Приучите ребенка периодически, по мере усталости, делать гимнастику для глаз. Убедите читать книги только за письменным столом с хорошим, желательно естественным, освещением.

Такими рекомендациями прежде все, по сути, и ограничивалось. Но сейчас этого мало. Наука расширила арсенал средств для профилактики глазных недугов. Это, главным образом, биологически активные добавки, обеспечивающие полноценное питание органа зрения. Такие средства позволяют избежать проблем с глазами, даже если нагрузки очень велики.

Вот например, капсулы "Окулист". В чем "изюминка" этого препарата? Прежде всего в том, что он содержат уникальные биофлавоноиды активные вещества, выделенные из лиственницы сибирской. Они раскрывают мелкие кровеносные сосудики глаз, закупоренные из-за стрессов или в силу возраста человека. А, следовательно, поддерживают в глазах нормальное кровоснабжение. И глаза сохраняют зоркость!

Учли разработчики "Окулиста" и то, что из-за агрессивных свободных радикалов естественная линза глаза с возрастом мутнеет, а зрение портится. Поэтому в состав капсул ученые ввели органический селен. Это был очень сильный ход. Селен надежно защищает и хрусталик, и сетчатку от повреждений, да и тормозит склерозирование сосудов.

А еще препарат содержит бета-каротин, необходимый для правильного цветовосприятия и хорошего сумеречного зрения. Но главное, конечно здесь много антоцианов черники, которые поддерживают работу сетчатки и улучшают ее чувствительность!

Но "Окулист" не просто единичный препарат. Разработчики создали целую линию для глаз. Вот, например, препарат для питания глаз "Окулист Черника". Он разрешен к применению уже с 4-х лет! Что выделяет его среди других биодобавок для зрения на основе черники? Огромное количество антоцианов. Даже сквозь пленку упаковки виден насыщенный "черничный" цвет его таблеток. Так что, антоцианов тут в избытке!

К тому же, "Окулист Черника" содержит множество витаминов и микроэле-ментов, которые при ежедневном приеме поддержат правильную работу глаз. В итоге удастся избежать зрительного переутомления, а риск снижения остроты зрения существенно уменьшается.

И что немаловажно, создавая препараты, ученые думали не только об их эффективности, но и о цене чтобы они были по карману всем. Это им удалось!

Не является лекарственным средством.

Ниманна-Пика болезнь, нистагм, новообразования слезного аппарата, Огути болезнь, ожоги глаз.

Ожог щелочью. Щелочи растворяют белок и вызывают коллимационный некроз без четко отграниченной зоны поражения. Образующийся щелочной альбуминат не препятствует дальнейшему проникновению повреждающего агента в глубь тканей. Это ведет к нарушению функции чувствительных и трофических нервов и к глубокой некротизации тканей. Разрушительное действие щелочи продолжается в последующие часы и даже дни после ожога. Поэтому тяжесть поражения щелочью не всегда может быть определена непосредственно после ожога. Ожог щелочью обычно протекает более тяжело, чем ожог кислотой. При этом конъюнктива и роговица поражаются сильнее, чем кожа век. Особенность ожога щелочью состоит еще и в том, что чем выше концентрация обжигающего раствора, тем меньшую болезненность он вызывает.
Скорая и неотложная помощь. Обильно промыть глаза водой до полного удаления из конъюнктивального мешка остатков ожигающего вещества: частицы обжигающего вещества тщательно Удалить с помощью увлажненного ватного тампона или пинцета. Повторно обильно промыть глаз водой и 0,1% раствором уксусной или 2% раствором борной кислоты. Обожженную кожу век смазать 10% мазью сульфапиридазин-натрия или стерильным рыбьим жиром. В конъюнктивальный мешок заложить 10% мазь сульфапиридазин-натрия, подкожно ввести 15003000 ME противостолбнячной сыворотки. При ожогах II, III, IV степени срочная госпитализация.

Ожог глаз известью. Ожог известью осложняется внедрением ее частиц в ткани глаза.
Скорая и неотложная помощь. При попадении в глаз гашеной извести срочно обильно промыть глаз струей проточной чистой воды в течение 1015 мин. Хорошо вывернув веки, влажным тампоном или пинцетом удалить частицы извести, оставшиеся после промывания. Промыть глаза 3% раствором динатриевой соли этилендиаминтетрауксусной кислоты (ЭДТА), которая связывает катионы кальция, образуя комплексы, растворимые в воде, легко вымываемые из тканей глаза. После промывания впускают раствор ЭДТА по 2 капли каждый час в течение суток. Подкожно ввести 1 5003000 ME противостолбнячной сыворотки. Госпитализация при ожогах глаз известью показана во всех случаях.
Медикаментозный ожог. По ошибке в конъюнктивальный мешок иногда впускают раствор йода, раствор нашатырного спирта и растворы других лекарственных средств. Для смазывания конъюнктивы могут, ошибочно воспользоваться карандашом ляписа. Эти ожоги вызывают сильную гиперемию кожи и конъюнктивы, иногда хемоз, эрозию или помутнение роговицы. После таких ожогов могут образоваться рубцы на коже, конъюнктиве и роговице.

Новости сайта Техники восстановления зрения: помоги себе сам.

7. По возможности использовать очки, защищающие от компьютерного излучения.

Не все очки и контактные линзы одинаковы.

Независимо от того, носите вы в данное время очки или нет, вы можете извлечь пользу из специальных компьютерных очков . Они помогут снизить зрительное напряжение и остановить ухудшение зрения, зачастую связанное с работой на компьютере.

Даже если вы постоянно не носите очки или линзы, компьютерные очки будут вам полезны, поскольку они помогут сохранить хорошее зрение.

Какой же тип компьютерных очков вам необходим? Попробуем разобраться.

В дополнение к использованию компьютерных очков , выполняйте все правила, изложенные в данной книге, они помогут вам повысить эффективность работы на компьютере. Если вы уже нуждаетесь в очках или линзах, правильное применение изложенных здесь принципов поможет вам постепенно снизить потребность в них.

Если вы носите очки или линзы для дали.

Большинство людей, нуждающихся в очках для дали, близоруки и видят без очков близлежащие объекты яснее, чем удаленные. Многие близорукие нормально видят ближние предметы без очков.

Однако если вы подолгу пользуетесь очками для дали, работая с близлежащими предметами, результатом этого могут стать частые стрессы, усталость, перенапряжение и снижение продуктивности. Почему? Потому что глазам сложнее сосредоточиться на близком объекте (которым является экран), если вы не снимаете очки для дали.

Более того, это приводит к ухудшению зрения и необходимости использования все более сильных очков.

Хорошо подобранные компьютерные очки для близоруких способны снизить напряжение, возникающее в процессе работы.

Компьютерные очки снижают напряжение мышц глаз при фокусировке на объекте, делая экранные символы чуть крупнее и отводя их чуть дальше.

Если вы носите очки или линзы для того, чтобы видеть вблизи.

Если вы носите очки для чтения, вы можете использовать их и при работе за компьютером. Очки для дальнозорких обычно прописываются для хорошего зрения на расстоянии примерно 40 сантиметров, но в случае с компьютером они могут являться не лучшим вариантом.

Если вы носите бифокальные очки, вы можете убедиться, что они непригодны для работы за компьютером. Вам приходится постоянно изгибать шею, а это только добавляет физическое напряжение и усиливает чувство дискомфорта, вызывает физическую и психическую усталость.

Зачастую при работе за компьютером лучше всего использовать специально разработанные для этого очки или линзы.

Если вы вообще не пользуетесь очками или линзами.

Если вы работаете за компьютером, но не носите очки, это не означает, что вы полностью избавлены от каких бы то ни было проблем со зрением.

Даже если вы не нуждаетесь в обычных очках, компьютерные очки помогут улучшить работоспособность и сохранят ваше зрение.

Если у вас возникают какие-либо зрительные или физиологические проблемы во время работы за компьютером, это должно настораживать.

Посоветуйтесь с поведенческим окулистом по поводу приобретения компьютерных очков .

Математика

Теория вектора Содержание: 1. Что такое вектор? 2. Сложение векторов. 3. Равенство векторов. 4. Скалярное произведение двух векторов и его свойства. 5. Свойства операций над векторами. 6. Доказательства и решение задач. Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике. Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике. В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики. Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрически подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрическо точки зрения - есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах. Итак, векторомназывается семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1). Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху, Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2

) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому. Различают начало и конец вектора (точнее, отрезка, изображающего вектор). Весьма часто понятию вектора дается другое определение: вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными. Векторы называются одинаково направленными, если их полупрямые одинаково направлены. Сложение векторов. Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную “геометрическую арифметику” – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе. Суммой векторов и с координатами а1, а2 и в1, в2 называется вектор с координатами а1 в1, а2 в2, т.е. Следствие: Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример. и – векторы (рис.5). Пусть 1. Строим параллелограмм оасв: АМ II ОВ, ВН II ОА. Для доказательства ассоциативности мы отложим от произвольной точки О вектор , от точки А вектор и от точки в – вектор с. Тогда мы имеем: откуда и следует равенство Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов. Остановимся теперь на случае, когда векторы и направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0. Равенство векторов. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине. И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны. Действительно, пусть векторы и – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор в вектор . Значит, векторы и равны, что и требовалось доказать. Скалярное произведение двух векторов и его свойства. Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.

Обозначение:. Свойства скалярного произведения: 1. х = х. 2. Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. х = 0. 3. Выражение х будем обозначать 2 и называть скалярным квадратом вектора . Свойства операций над векторами. Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме. 1. Пусть даны = (ах, аy, аz) и = ( вx, ву, вz), тогда сумма этих векторов есть вектор , координаты которого равны сумме одноименных координат слагаемых векторов, т.е. = = (ах вx; аy ву; аz вz). Пример 1. = ( 3; 4; 6) и = ( -1; 4; -3), тогда = ( 3 ( -1); 4 4; 6 (-3)) = ( 2; 8; 3). 2. = (ах, аy, аz) и = ( вx, ву, вz), тогда разность этих векторов есть вектор , координаты которого равны разности одноименных координат данных векторов, т.е. = - = (ах - вx; аy - ву; аz - вz). Пример 2. = ( -2; 8; -3) и = ( -4; -5; 0), тогда с = – = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = ( 2; -13; -3). 3. При умножении вектора = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. м = ( мах, маy, маz). Пример 3. = ( -8; 4; 0) и м = 3, тогда 3 = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0). Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач. Рассмотрим доказательство некоторых теорем с помощью векторов. Теорема 1. Диагонали ромба взаимно перпендикулярны. Доказательство. Пусть авсd – данный ромб (рис.7). Введем обозначения: Из определения ромба: По определению суммы и разности векторов Рассмотрим .   Так как стороны ромба равны, то =. Следовательно, Из последнего получаем Ч.т.д. Рассмотрим теперь решение задач с помощью векторов. Задача 1. Даны два вектора и , причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2; 1;5). Определить, перпендикулярны они друг другу или нет. Решение. Найдем сначала координаты векторов. = ( -3; 3; 0) и = (3; 3; 3). Вычислим теперь скалярное произведение этих векторов: х = ( -3) х 3 3 х 3 0 х 3 = 0. Последнее и означает, что Задача 2. Дан произвольный треугольник авс. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника авс. Решение. Обозначим медианы треугольника авс через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника авс, через а, в, с: = а, = в, = с (рис.8). Тогда АD =AB ВD =AB = с аналогично определяются и другие медианы: = а , = в Так как, в силу условия замкнутости = а в с =0, то мы имеем: = ( с ) (а ) ( в ) = ( а в с) = х 0 = 0. Следовательно, отложив от точки В, вектор и от точки С1 – вектор , мы получим. А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1. Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.

Можно разделить все проблемы философии науки на три подвида. К первым относятся проблемы, идущие от философии к науке, вектор направленности которых отталкивается от специфики философского знания. Поскольку философия стремится к универсальному постижению мира и познанию его общих принципов, то эти интенции наследует и философия науки. В данном контексте она занята рефлексией над наукой в ее предельных глубинах и подлинных первоначалах. Здесь в полной мере используется концептуальный аппарат философии, необходимо наличие определенной мировоззренческой позиции. 172 Вторая группа возникает внутри самой науки и нуждается в компетентном арбитре, в роли которого оказывается философия. В этой группе очень тесно переплетены проблемы познавательной деятельности как таковой, теория отражения, когнитивные процессы и собственно "философские подсказки" решения парадоксальных проблем. К третьей группе относят проблемы взаимодействия науки и философии с учетом их фундаментальных различий и органичных переплетений во всех возможных плоскостях приложения

1. Теории и гипотезы о Луне

2. Происхождение человека. Эволюция человека. Теории и гипотезы

3. Теории зарождения жизни на Земле

4. Теория Дарвина

5. Антропогенез: эволюционная теория происхождения человека

9. Противоречивость "норманнской теории" происхождения государства у славян

10. Норманнская теория происхождения русской государственности ее апологеты и критики

11. Шпаргалка по общей теории права

12. Теория государства и права как наука и учебная дисциплина

13. Генезис (развитие) теории правового государства с древнейших времен и по наши дни

14. Теории государства и права (Шпаргалка)

15. Теория государства и права

16. Теория государства и права

17. Теория государства и права (Шпаргалка)

18. Теория разделения властей

19. Экзаменационные вопросы к государственному экзамену по теории государства и права

20. Определения (Теория государства и право)

21. Предмет теории государства и права

25. Теория государства и права (тгп) в таблице

26. Теория государства и права (шпаргалки)

27. Теория и методика преподавания классического танца

28. Антропогенез: эволюционная теория происхождения человека

29. Проблемы теории культуры в отечественной философии (А. Ф. Лосев, М. К. Мамардашвили)

30. Шпоры по Поэтике или теории литературы

31. Теория и методика русского языка (экзаменационные билеты)

32. Норманнская теория происхождения государства у славян и ее роль в российской истории

33. Краткий конспект лекций по Теории тестирования аппаратных и программных средств

34. Теория системного управления

35. Постановка лабораторной работы по теории графов

36. Теория многозадачности и многопоточности

37. Лекции по теории проектирования баз данных (БД)

41. Лабораторная работа №3 по "Основам теории систем" (Теория двойственности в задачах линейного программирования)

42. Лабораторная работа №6 по "Основам теории систем" (Решение задачи о ранце методом ветвей и границ)

43. Достаточно общая теория управления (Расовые доктрины в России: их возможности и целесообразность следования им в исторической перспективе)

44. Теория систем автоматического регулирования

45. Теория устойчивости

46. Теория вероятностей и случайных процессов

47. Основы теории систем и системный анализ

48. Теория вероятностей и математическая статистика

49. Моделирование значений случайных векторов

50. Теория статистики (Станкин)

51. Теория графов. Методические указания по подготовке к контрольным работам по дисциплине «Дискретная математика»

52. Теория вероятности решение задач по теории вероятности

53. Теория мышления, интеллектуальные различия, лобные доли

57. Теории обучения в высшей школе

58. Психологические теории эмоций

59. Теория и методика воспитания (шпаргалка)

60. Теория международных отношений

61. Теория мертвой страны

62. Теория политических решений

63. Теории деформационного упрочнения монокристаллов

64. Основы теории надежности

65. Гидродинамическая теория смазки и ее возможности для расчета и анализа работы подшипников двигателя внутреннего сгорания

66. Теории о несуществовании загробного бытия

67. Культурологическая и психосексуальная теория Фрейда

68. Ортодоксальность теории З. Фрейда

69. Основные теории мотивации

73. Экзистенциальный анализ. История, теория и методология практики

74. Изучение теории личности и межличностных отношений

75. Теория социально-психологическог тренинга

76. Теория лжи

77. Теория установки Узнадзе

78. Основы теории цепей

79. Теории электрической связи: Расчет приемника, оптимальная фильтрация, эффективное кодирование

80. 6 задач по теории электрических цепей

81. Иудаизм - теория и практика расизма

82. Времяоника. Теория, которой суждено изменить жизнь человечества

83. Теория лидерства

84. История теорий социального неравенства

85. Теория конфликтов. Проекция на сферу управления

89. Некоторые парадоксы теории относительности

90. Теориям самоорганизации - синергетика, теория изменений и теория катастроф

91. Развитие взглядов на теорию света

92. Плоская задача теории упругости

93. Суперструны и М-теория

94. Основы теории измерений (спортивная метрология)

95. Теория Николая Коперника

96. Философские аспекты теории относительности

97. Л. Дюги. Теория социальной солидарности

98. Философские аспекты теории относительности А. Эйнштейна

99. Плебисцитарная теория демократии Макса Вебера и современный политический процесс

Следующие статьи

• Подбор контактных линз при астигматизме. Подбор контактных линз при афакии. Подбор контактных линз при кератоконусе.
• Глаз, мозг, зрение Хьюбел Д. Глаза — не только зеркало души. Глаза должны быть красивыми.
• Строение глаз. Строение глаза. Строение глаза и его работа.

Поделитесь своим мнением

Имя *

Почта *

Тект *

Сумма цифр:

Индометацин

Как лечат глаза в Израиле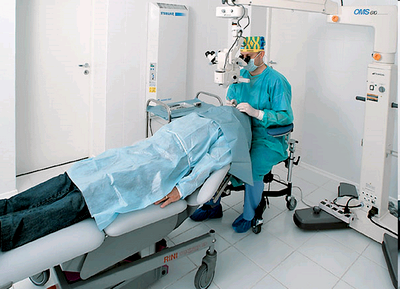

Сколько стоит операция катаракта глаза в москве

Интересное:

Макияж смоки айс для зеленых глаз свадебный

Катаракта операция стоимость одесса ольгиевская

Карандаш подводка для глаз с растушевкой